- マルホ発條工業株式会社
- Mnet会員サービス
- ばね設計解説
- 薄板・細工ばねの計算
薄板・細工ばねの計算

| 記号 | 意味 | 単位 |
|---|---|---|
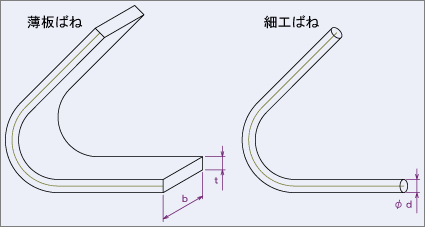
| t | 材料の板厚(薄板ばね) | mm |
| b | 材料の板幅(薄板ばね) | mm |
| d | 材料の直径(細工ばね) | mm |
| I | 断面二次モーメント | mm4 |
| Z | 断面係数 | mm3 |
| E | 縦弾性係数 | N/mm2、MPa |
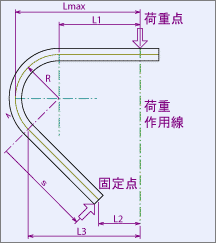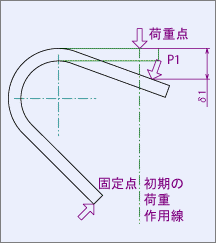
| L | 荷重作用線に垂直方向の長さ | mm |
| Lmax | 最大曲げ応力点距離 | mm |
| s | 直線梁成分の梁長さ | mm |
| R | 円弧梁成分の曲げR | mm |
| Λ | ばねの軸線の、荷重作用線に対する二次のモーメント | mm3 |
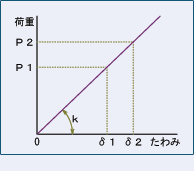
| δ(δ1、δ2) | たわみ(2点指定) | mm |
| P(P1、P2) | 荷重(2点指定) | N |
| k | ばね定数 | N/mm |
| σ(σ1、σ2) | 曲げ応力(2点指定) | N/mm2、MPa |
| σB | 材料の引張強さ | N/mm2、MPa |
| ばね定数 | |
|---|---|
 |
 |
ばねの設計に用いる“縦弾性係数E”の値は、原則として以下による。
| 材質 | 縦弾性係数E |
|---|---|
| 硬鋼線・ピアノ線 | 196,000MPa |
| オイルテンパー線 | 196,000MPa |
| オーステナイト系ステンレス鋼線 | 176,400MPa |
| 析出硬化型ステンレス鋼線 | 184,240MPa |
| 黄銅線 | - - - |
| 洋白線 | - - - |
| りん青銅線 | 107,800MPa |
| ベリリウム銅線 | - - - |
薄板ばね及び細工ばねの設計に用いる設計公式は、以下の通りである。
- 断面二次モーメント:I


- 断面係数:Z
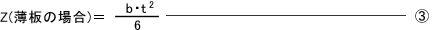
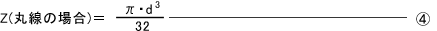
- ばね定数:k
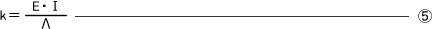
- 曲げ応力:σ

- ばねの軸線の荷重作用線に対する二次のモーメント:Λ

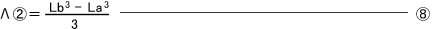



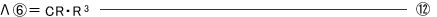
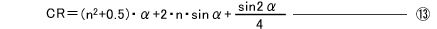

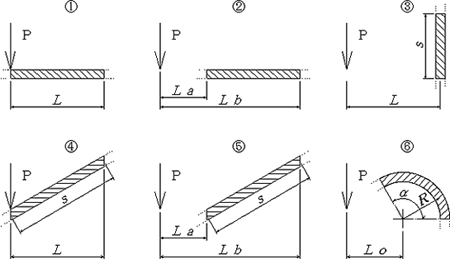
薄板ばね及び細工ばねの設計において考慮すべき主な事項は、以下の通りである。
- ばね特性
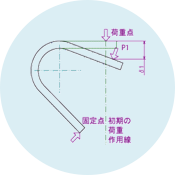
薄板ばね及び細工ばねは、材料の曲げ弾性を利用するため、荷重値は、板厚の3乗(薄板の場合)、あるいは線径の4乗(丸線の場合)に比例する。従って、板厚あるいは線径のわずかな差が、荷重値に大きな影響を与えることになる。 荷重値は、材料の縦弾性係数Eに比例するが、Eの推定値には、2~3%程度の誤差は必ず含まれる。 薄板ばね及び細工ばねは、負荷により変形してばね定数が変化する。従って、自由時の形状から求めたばね定数は、初期(自由時)のばね定数を表しているにすぎない。 以上の理由から、数字上の精密な計算はあまり意味を持たず、荷重特性の許容差が厳しい場合には、試作と実機での評価が必要になる。 - 形状(ばねの軸線の荷重作用線に対する二次のモーメント:Λ)
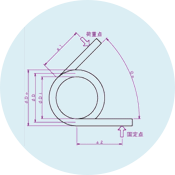
薄板ばね及び細工ばねは、その形状が多種多様であるため、コイルばねのような設計の定形式と言えるものがない。従って、計算しようとするばねの形状に合わせて、その都度、新たに設計式を構築する必要があるが、この設計式の構築が、“ばねの軸線の荷重作用線に対する二次のモーメント:Λ”の計算に該当する。 Λは、ばねの側面の形によって決まる係数であり、全体を、直線からなる部分と円弧からなる部分に適当に分割した後、各分割部分のΛを求めれば、それらを合算することにより、全体のΛを求めることが出来る。 具体的には、まず、荷重作用線で左右に分割し、さらに直線部は屈曲点で、円弧部はその中心を通り荷重線に垂直な直線で上下に分割する。 また、Λは、二次のモーメントであるから、下図の如く、荷重作用線に対して対称な形のΛ、および荷重作用線に垂直な直線に対して対称な形のΛは、全て同じ値となり、同一の計算式で算出することが出来る。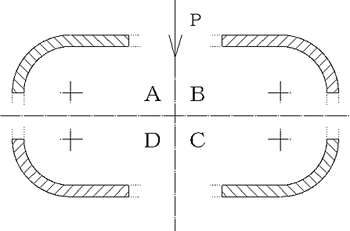
- 応力:σ
薄板ばね及び細工ばねは、荷重の負荷に伴い、ばねに曲げモーメントが作用するため、曲げ応力が最大となるのは、ばねの構成要素内で、荷重作用線より最も遠い部分となる。 よって、荷重作用線からこの最遠要素までの荷重作用線に垂直な方向の距離(Lmax)に、荷重作用線上に負荷された荷重値(P)を乗したもの(曲げモーメント)を、最遠要素部分の断面係数(Z)で除すれば算出できる。